Mục Lục Nội Dung
Animation và Trace là hai tính năng rất thường được sử dụng trong phần mềm vẽ hình – hình học động GeoGebra. Và người ta thường sử dụng chúng để để mô tả bài toán, mô hình bài toán, …
Vâng, và ở trong bài viết này mình sẽ hướng dẫn cho các bạn sử dụng tính năng Animation và Trace để mô hình hóa khái niệm hình nón với phần mềm GeoGebra.
Để có thể xây dựng được mô hình này yêu cầu tiên quyết là bạn phải biết sử dụng GeoGebra ở mức cơ bản đặc biệt là phải biết vẽ hình trong không gian 3 chiều.
Nếu bạn mới tiếp xúc với phần mềm GeoGebra thì bạn nên tham khảo serie hướng dẫn cách sử dụng phần mềm GeoGebra có trên Blog nhé!
#1. Khái niệm hình nón và ý tưởng sư phạm
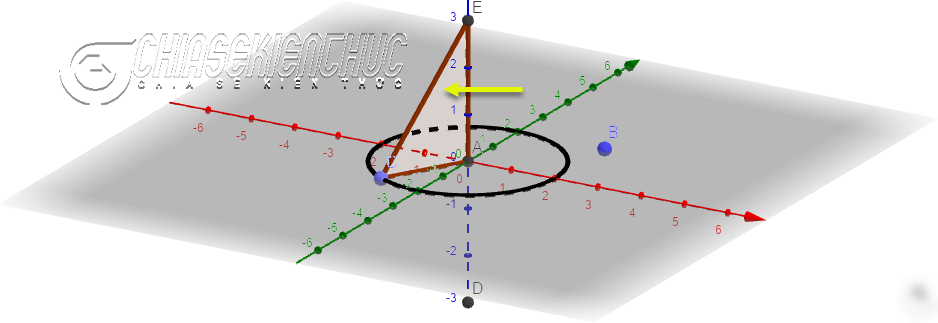
Như các bạn có thể thấy, khi quay tam giác vuông AOC một vòng quanh cạnh góc vuông OA cố định thì ta được một hình nón.
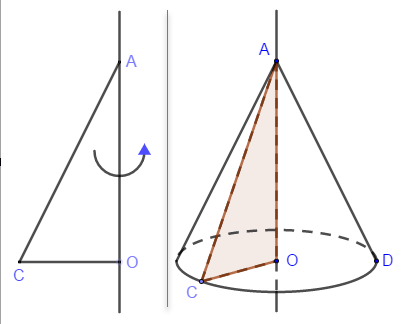
Ý tượng sư phạm ở đây là chúng ta sẽ đi dựng một đường tròn tâm O, dựng tam giác vuông AOC, sau đó bật lệnh Show Trace cho tam giác, bật lệnh Animation cho điểm C
Khi đó C sẽ chuyển động quanh đường tròn, C mà chuyển động sẽ kéo tam giác chuyển động theo. Vì tam giác đã được hiển thị vết nên khi C chuyển động được một vòng ta sẽ thu được một hình nón.
=> Từ đó giáo viên sẽ gợi ý, hướng dẫn để học sinh có thể phát biểu được khái niệm một cách rất dễ hiểu !
#2. Các bước mô hình hóa khái niệm hình nón
Mô hình hóa là gì? Mô hình hóa (Modeling) là thay thế đối tượng gốc bằng một mô hình nhằm thu nhận thông tin quan trọng về đối tượng bằng cách tiến hành các thực nghiệm trên mô hình. Lý thuyết xây dựng mô hình và nghiên cứu mô hình để hiểu biết về đối tượng gốc gọi lý thuyết mô hình hóa.
+ Bước 1: Vì hình nón là một đối tượng thuộc không gian 3 chiều nên chúng ta cần chọn ngữ cảnh làm việc là 3D Graphics.
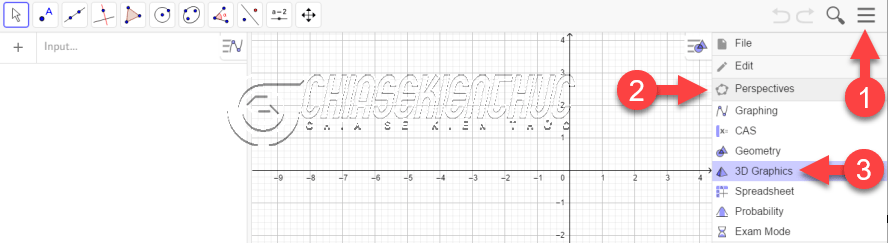
Thực hiện: Bây giờ bạn hãy khởi động phần mềm GeoGebra lên => chọn vào biểu tượng “ba dấu gạch ngang” => chọn Perspectives => chọn 3D Graphics
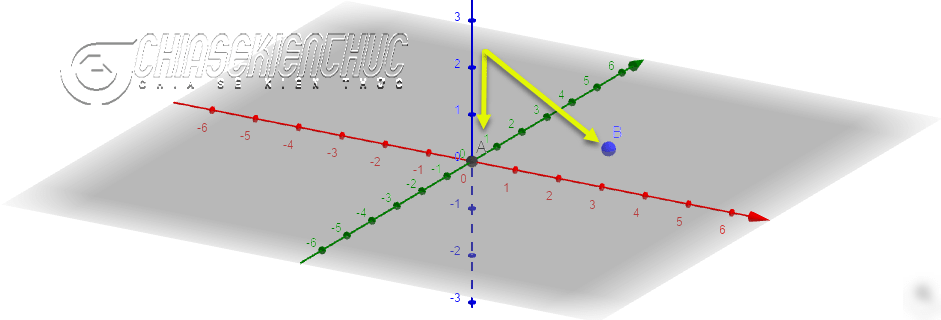
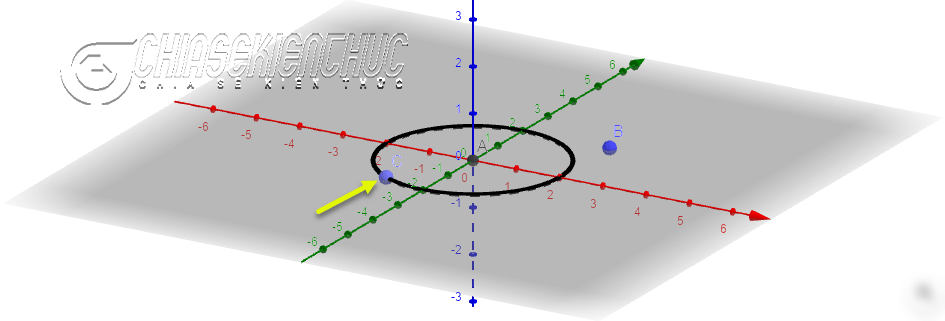
+ Bước 2: Dựng hai điểm A và B nằm trên mặt phẳng Oxy. Chọn công cụ Point => nháy chuột vào mặt phẳng Oxy
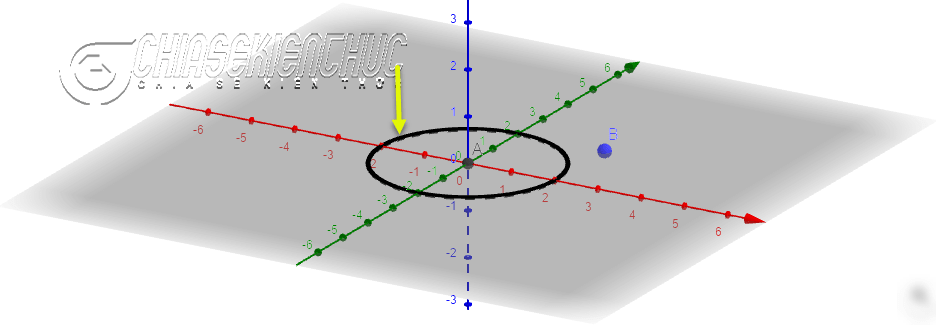
+ Bước 3: Dựng đường tròn tâm A, nằm trên mặt phẳng Oxy và có bán kính là a (a là một số tự nhiên khác 0)
=> Chọn vào công cụ Circle with Center Radius and Direction => nháy chuột vào điểm A, điểm B => nhập bán kính là a => chọn OK => chọn Create Sliders.
+ Bước 4: Dựng điểm C thuộc đường tròn. Chọn công cụ Point on Object => nháy chuột vào đường tròn..
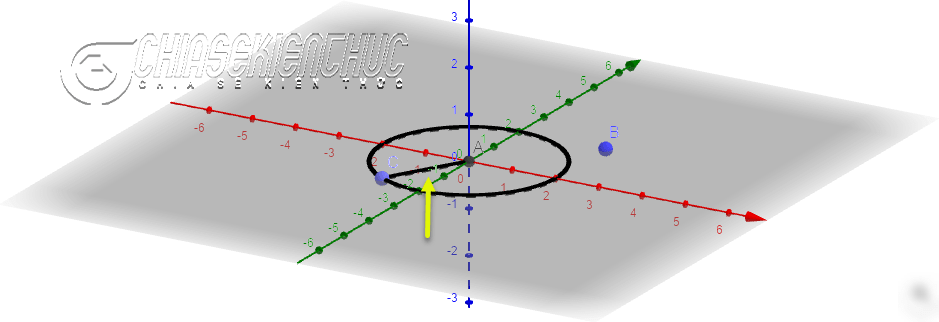
+ Bước 5: Dựng đoạn thẳng AC. Chọn công cụ Segment => chọn điểm A => chọn điểm C
+ Bước 6:
- Dựng đường thẳng đi qua điểm
Avà vuông góc với mặt phẳngOxy - Dựng hình cầu tâm
A, bán kính1.5a - Dựng giao điểm của đường thẳng và hình cầu.
Chọn công cụ Perpendicular Line => chọn điểm A => chọn mặt phẳng Oxy
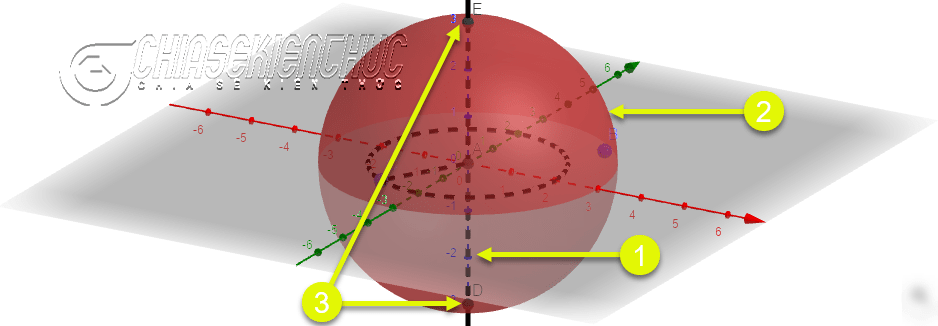
===>>> Chọn công cụ Sphere: Center & Radius => chọn điểm A => nhập bán kính là 1.5a ===>>> Chọn công cụ Intersect => chọn hình cầu => chọn đường thẳng.
+ Bước 7: Vì đoạn thẳng AC, đường thẳng và hình cầu là đối tượng phụ nên chúng ta sẽ ẩn nó đi.
Nháy chuột phải vào đoạn thẳng AC => bỏ chọn Show Object => nháy chuột phải vào đường thẳng => bỏ chọn Show Object => nháy chuột phải vào hình cầu => bỏ chọn Show Object.
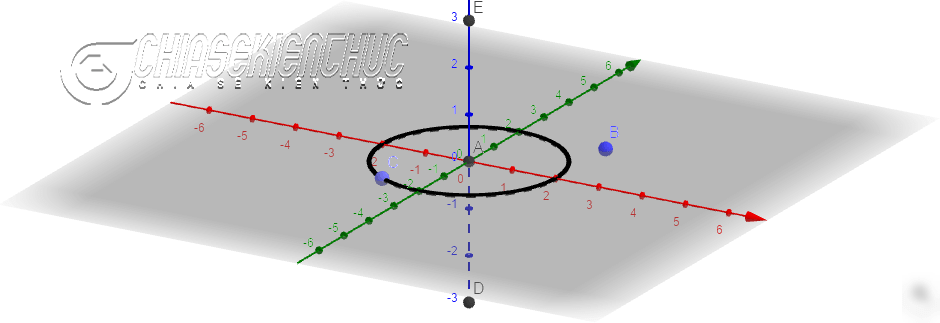
+ Bước 8: Dựng tam giác ACB. Chọn công cụ Polygon => sau đó chọn điểm A, C, E, A
+ Bước 9:
- Thực hiện tương tự như
Bước 7để ẩn các đối tượng phụ còn lại như điểmB, đường tròn, điểmD - Đổi tên điểm A, C, E lần lượt thành O, C, A
- Ẩn mặt phẳng Oxy và hệ trục tọa độ.
Nháy chuột phải vào điểm A => chọn Rename => nhập O => chọn OK => … (đổi tên điểm C và E) ===>>> Nháy chuột phải vào mặt phẳng Oxy bỏ chọn Axes => bỏ chọn Plane.
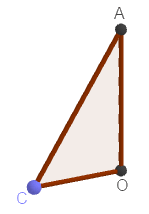
+ Bước 10:
- Tạo vết cho tam giác
AOC - Tạo chuyển động cho điểm
C
Nháy chuột phải vào tam giác AOC => chọn Show trace ===>>> Nháy chuột phải vào điểm C => chọn Animation
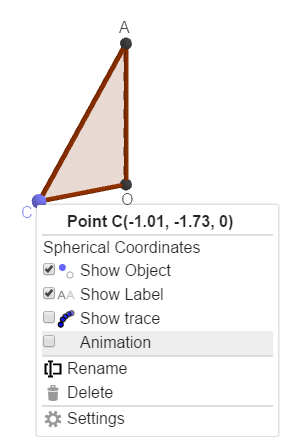
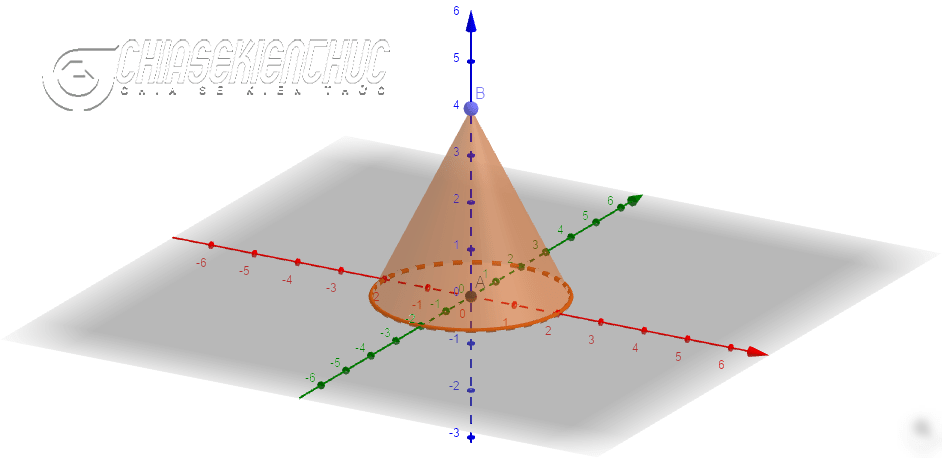
Ngay khi bạn chọn Animation thì điểm C sẽ chuyển động => kéo theo tam giác AOC chuyển động theo, và khi C chuyển động được một vòng thì hình nón sẽ được vẽ ra..
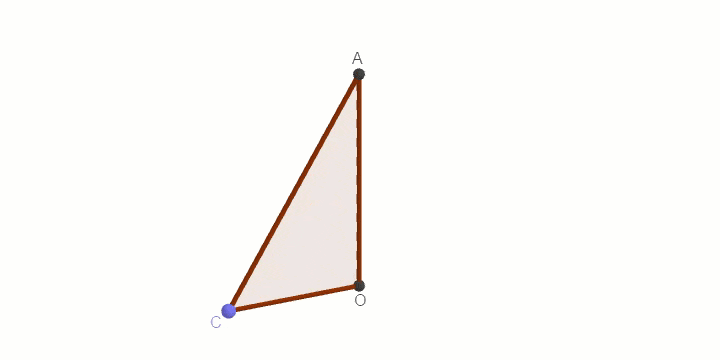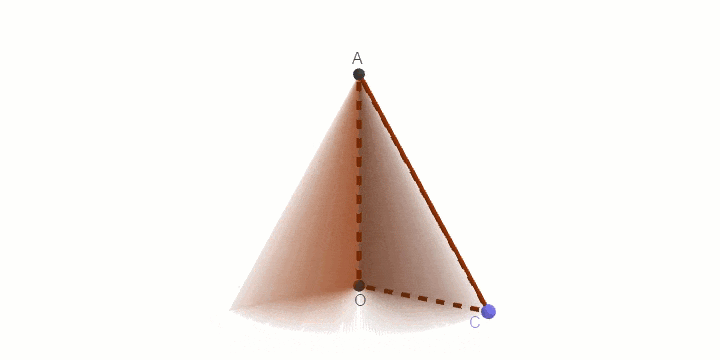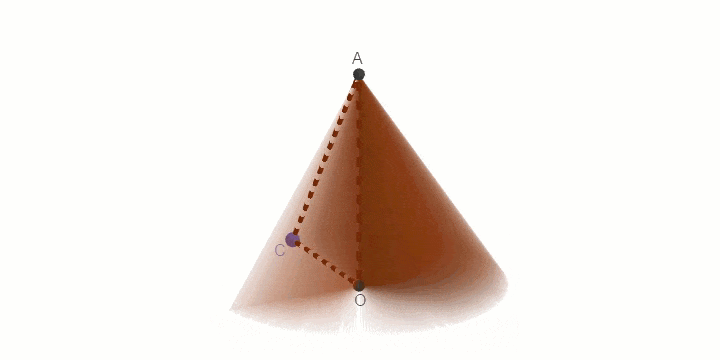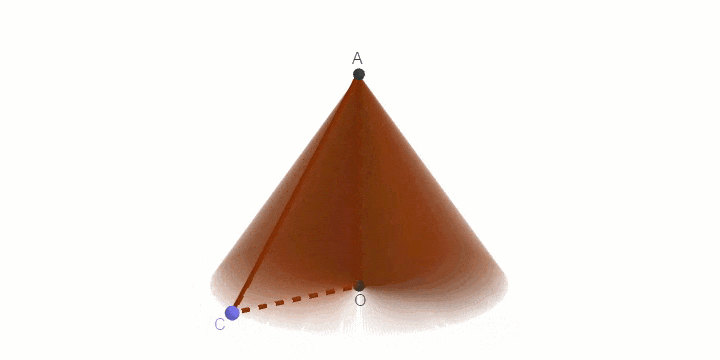
Để dừng chuyển động thì bạn chỉ cần nháy chuột phải vào điểm C => bỏ chọn Animation là được.
#3. Vẽ hình nón trong không gian 3 chiều
Hình nón được vẽ theo cách trên thường chỉ được sử dụng khi chúng ta cần số hóa khái niệm. Việc làm này giúp học sinh dễ dàng nắm bắt, phát biểu và nhớ được khái niệm hơn.
Còn trong trường hợp chỉ cần vẽ một hình nón đơn giản để minh họa thì bạn chỉ cần thực hiện theo hai bước bên dưới:
+ Bước 1: Chọn vào công cụ Cone
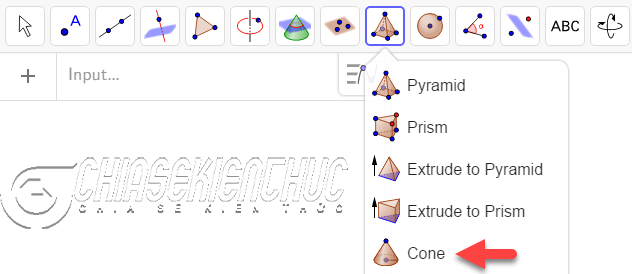
+ Bước 2: Di chuyển chuột đến vị trí thích hợp rồi nháy chuột để tạo hai điểm => nhập bán kính.
#4. “Vẽ hình nón trên mặt phẳng”
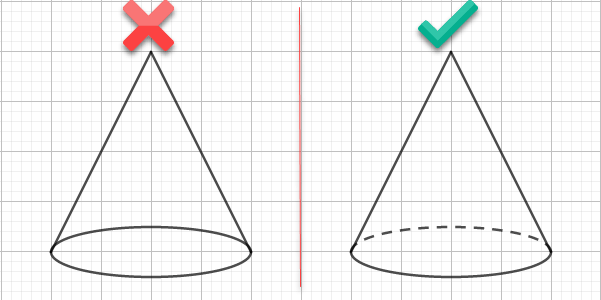
Hình Ellipse có nửa trên là nét đứt, nửa dưới là nét liền – nói chung là khá khó vẽ và nó cũng có khá nhiều bước. Vì vậy mà trong thực tế có nhiều giáo viên, sinh viên và học sinh vẽ hình nón như hình bên trái.
Dễ thấy hình bên trái là không chính xác bởi vì nửa Ellipse trên là phần bị chắn nên phải vẽ bằng nét đứt như hình bên phải mới đúng.
“Vẽ hình nón trên mặt phẳng” chỉ có một bước khó duy nhất đó là vẽ hình Ellipse có nửa trên là nét đứt. Về cách vẽ thì mình đã hướng dẫn rất chi tiết trong bài viết Ứng dụng phần mềm GeoGebra trong việc dạy Toán học
Các bước vẽ còn lại không có gì khó khăn cả, bạn tham khảo bài viết trong link liên kết đó nếu chưa biết cách làm nhé !
#5. Lời kết
Vâng, như vậy là mình đã hướng dẫn xong cho bạn cách sử dụng phần mềm GeoGebra để mô hình hóa khái niệm hình nón rồi ha.
À quên ! Ở đây có thể bạn đang thắc mắc là tại sao đường tròn lại có bán kính là a, còn bán kính của hình cầu lại là 1.5a phải không?
Câu trả lời rất đơn giản, nhập bán kính là a để GeoGebra tự động tạo ra thanh trượt, khi cần thay đổi bán kính ta chỉ việc kéo thả thanh trượt này là được.
Còn về hằng số 1.5 thì chỉ là sự lựa chọn ngẫu nhiên, bạn chọn bao nhiêu cũng được (ngoại trừ 1) miễn sao hình nón của bạn cân đối, giúp học sinh dễ dàng quan sát là được.
Ngoài ra, nếu không thích a thì bạn cũng có thể chọn một số thực dương bất kì để đơn giản thao tác xây dựng mô hình. Okay, xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Note: Bài viết này hữu ích với bạn chứ? Đừng quên đánh giá bài viết, like và chia sẻ cho bạn bè và người thân của bạn nhé !
Xem Chi Tiết Ở Đây >>>
Bạn có thể quan tâm:
>> Năm lý do khiến bạn nên mua một chiếc AirPods Max
>> Tai nghe Galaxy Buds2 đang được chế tạo, thiết kế có nhiều nâng cấp
>> Loa 7.1 Là Gì? Hệ Thống Âm Thanh 7.1 Được Sắp Xếp Như Thế Nào?


0 nhận xét:
Đăng nhận xét